【ナッシュ均衡とは】囚人のジレンマ・パレート最適との関係からわかりやすく解説

アメリカの数学者ジョン・ナッシュによって、提唱されたゲーム理論における重要なテーマのひとつでです。

経済学だけでなく社会科学全体と関連する概念ですので、その概要を知っておくことは非常に重要ですし、さまざまな社会現象を分析する手段の1つになります。

そこでこの記事では、

• ナッシュ均衡の意味
• ナッシュ均衡と囚人のジレンマ・パレート最適

について解説します。

好きな箇所から読み進めてください。

1章：ナッシュ均衡とは

１章ではナッシュ均衡を概説します。囚人のジレンマやパレート最適との関係を知りたい方は、２章以降から読み進めてください。

1-1: ナッシュ均衡の意味

ナッシュ均衡とは、アメリカの数学者ジョン・ナッシュによって提唱されたゲーム理論における重要なテーマのひとつです。

ゲーム理論に関する詳しい説明は割愛しますが、利害関係を持つ相手がいる状況で、自分と相手の利益を考え、最適な行動を決めるための理論のひとつであると認識してください。

ゲーム理論的な考え方は、さまざまな経済問題を考えるうえで非常に重要です。とりわけ経済学では、「需要者」対「供給者」「自社」対「他社」「自国」対「他国」など利害が異なる対立関係が頻繁に登場します。

ナッシュ均衡は、こうしたゲームに共通する基本的な均衡概念を示した理論であり、ゲーム理論ならびに経済学に大きな発展をもたらした理論であると言われています。

簡易な定義を述べるのが難しいナッシュ均衡ですが、経済学者の伊藤元重はナッシュ均衡を次のようにまとめています²伊藤元重『はじめての経済学[上]』日本経済新聞出版社 174頁。

各ゲームのプレーヤーは、それぞれが合理的な行動をとることを想定して相手の行動を知ろうとしたときに、自分にとって最も好ましい行動を取ろうとします。それぞれがそれぞれにとって最も合理的な行動をとろうとした結果、実現した状態があれば、そこからだれも行動の変更をしようとはしないと考えられるからです。

この説明だけでナッシュ均衡を理解するのは難しいと思いますので、以下で詳しく解説していきます。

1-2：ゲーム理論とナッシュ均衡

ナッシュ均衡の説明を理解するために、典型的な国家間の競争を例にあげてゲーム理論とナッシュ均衡を考えていきましょう。

世界中の国々を巻き込んだ国家間競争といえば、第二次世界大戦後から50年近くにもわたって続いたアメリカ合衆国とソビエト連邦共和国の冷戦です。

それぞれが経済対策にかける支出を削減してまでも国防支出を増加させていったのは、両国の対立がゲーム理論のエッセンスとも言える２つの要素を兼ね備えていたからでした。

第一に、相互の行動が相手に影響を及ぼすという意味での相互の依存関係が存在していたことです。冷戦下において、両国にとっての軍事的な遅れとは相手に攻撃の隙を与えることと同義であり、安全保障の面で対等以上であり続けることが必須条件でした。

もし、片方の国が莫大な国防支出を投じ、画期的な戦略兵器を開発できたとしたら、その兵器に対抗するためにもう片方の国はそれ以上に国防支出を投じ、新たな戦略兵器を開発するという相互依存が定着したことで終わりの見えない軍拡競争が続くことになりました。

第二に、個々の主体が自分にとって最も合理的な結果になるように行動していたことです。ここでいう自分にとって最も合理的な判断にも、ひとつめの要素である相互の依存関係が深く関与します。

たとえば、10という国家予算の使い道を考える際に、費用対効果を考えた振り分けはとても重要です。

冷戦期に幾度となく双方の軍縮協議がおこなわれている事実からも、こうした一見不合理な判断が頻繁にされていたことが推測されます。

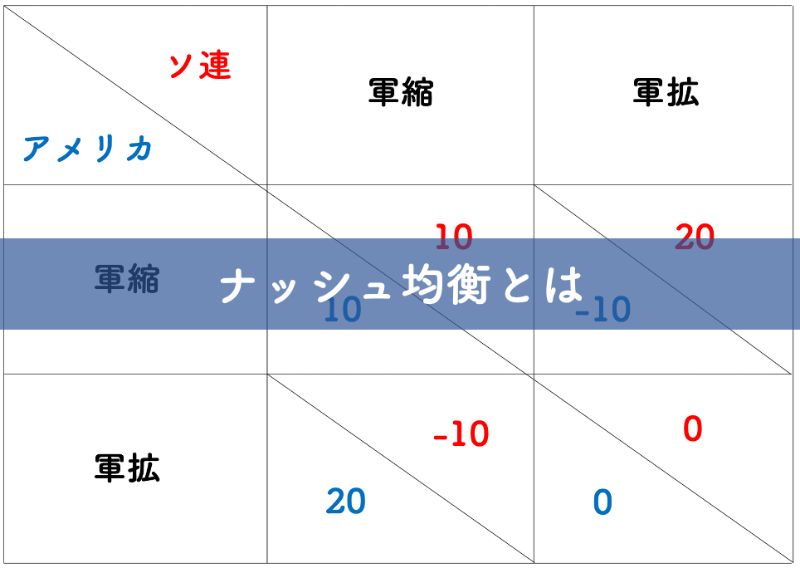
冷戦のケースを参考にゲーム理論のポイントが少し理解できたところで、ナッシュ均衡とはなにかを見ていきましょう。図1は上記にまとめた要素を参考に、アメリカとソ連のそれぞれの行動とその利得を表した図表です。

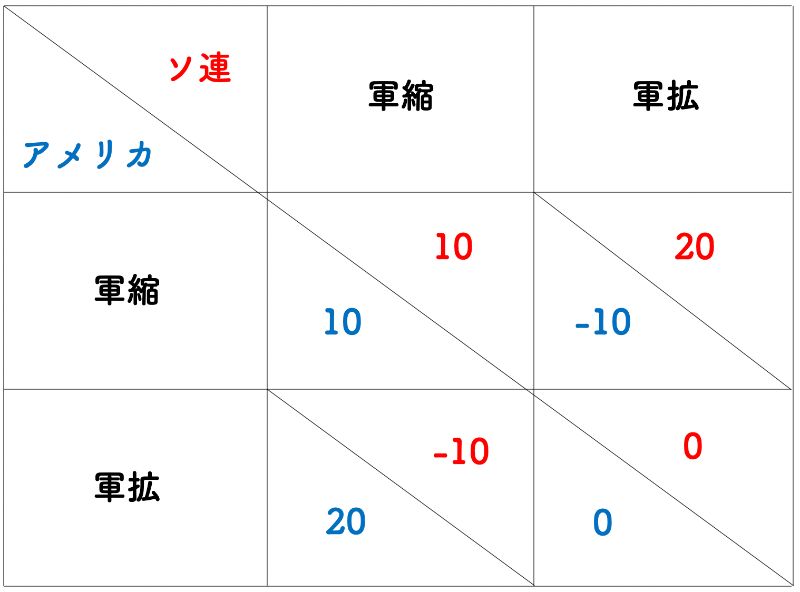（図１「冷戦中のゲーム理論モデル」出典: 筆者作成）

数字自体に特別な意味はありません。ですが、マイナスの数字はその行動が主体にとってデメリットに働き、プラスの数字は主体にとってプラスに働くと考えてみてください。また、それぞれの数字が大きいほど、その行動の影響は大きくなり、もしゼロであれば双方にとってメリットもデメリットもないとします。

このように仮定したとき、以下のような状況を説明することができます。

上述したように、ナッシュ均衡とは「各ゲームのプレーヤーは、それぞれが合理的な行動をとることを想定して相手の行動を知ろうとしたときに、自分にとって最も好ましい行動を取ろうと」することを指します。

そこで、ナッシュ均衡を考える上では、先に相手の行動を想定し、そこから自らの行動を決めるという解法が採用されます。実際に、図１を使ってナッシュ均衡を求めてみましょう。

それぞれの国の選んだ行動をまとめると図2のようになります。図２からもわかるように、どちらの国も「軍縮」の行動をとる可能性はなく、ゲーム理論上では「軍拡」のみが双方に与えられた選択肢となります。

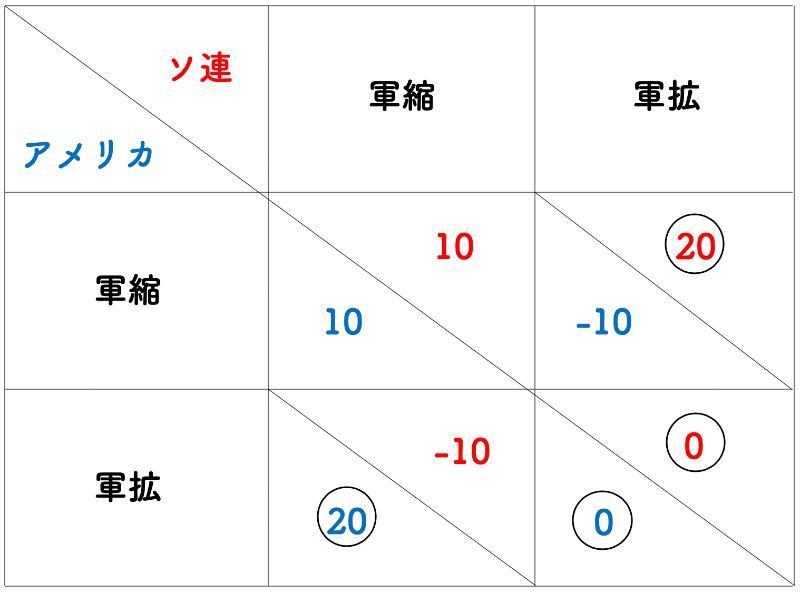
（図２「冷戦中のゲーム理論モデルにおけるナッシュ均衡」出典: 筆者作成）

ここで、上述のナッシュ均衡の説明の後半部分を見てみましょう。

それぞれがそれぞれにとって最も合理的な行動をとろうとした結果、実現した状態があれば、そこからだれも行動の変更をしようとはしないと考えられる

図２において、「それぞれにとって最も合理的な行動」とは「軍拡」に他なりません。つまり、アメリカが「軍拡」という行動を取り、ソ連が「軍拡」という行動を取るという現象が、このゲームにおける「ナッシュ均衡」に該当するのです。

２章では、ナッシュ均衡とも関わりの深い「囚人のジレンマ」についても触れつつ、ナッシュ均衡をもう少し深堀していきます。

いったん、これまでの内容をまとめます。

2章：ナッシュ均衡と囚人のジレンマ

ゲーム理論におけるもっとも有名な事例で、ゲーム理論の説明には必ずと言って良いほど登場するのが「囚人のジレンマ」です。「囚人のジレンマ」という名前からもわかるように、この事例では２人の囚人が登場します。

下記の図３は、「囚人のジレンマ」を表した関係図です。図３は以下のように読み解いてください。

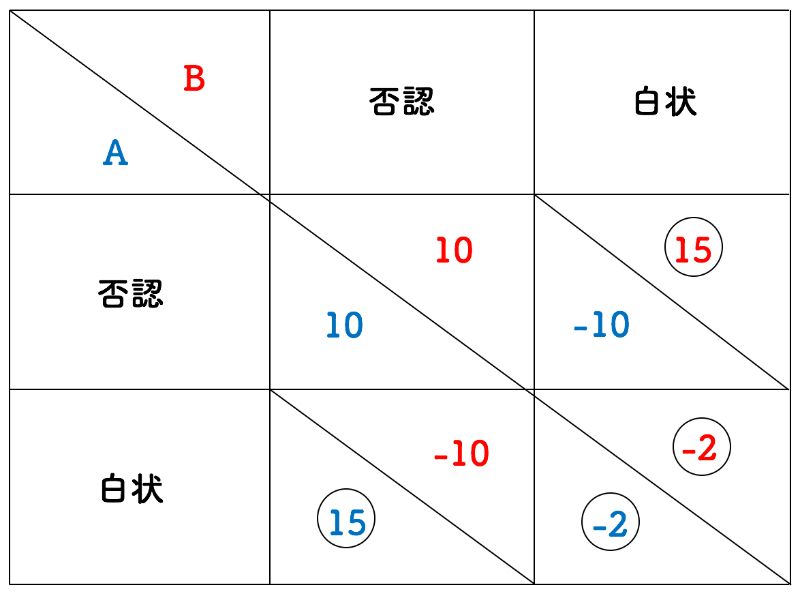（図３「囚人のジレンマ」出典: 筆者作成）

ではここで、1章と同じように、相手の立場に立って2人の囚人の選択を考えてみましょう。

先に相手の行動を想定し、そこから自らの行動を決めると仮定すると、選択されうるのは図2において〇のついた選択肢となります。つまり、与えられた図２の条件下では、どちらのプレーヤーも「白状」しか選ばないことがわかります。

ゲーム理論では、相手の行動によって自分の行動が変化せず、常に同じ行動をしてしまうことを行動主体にとっての「支配戦略」と呼びます。そして、【2人とも白状する】という双方にとってマイナスになる選択肢のみが、互いに一致する選択肢であることわかります。

したがって、囚人のジレンマでは、

ことがわかります。これが「囚人のジレンマ」と呼ばれる所以です。

ここで重要なのは①互いにコミュニケーションが取れないこと、②相手の行動を思いめぐらせながら自分の行動を決めること、の２点です。

もし、①の条件がなければ、互いに連携して【2人とも否認する】という双方にとって利得の大きい選択肢を採用するでしょうし、②の条件がなければ、【どちらかが白状し、もう片方は否認する】という、自分のみ利得が最大になる選択肢を採用することでしょう。

※囚人のジレンマについて詳しくはこちら
→【囚人のジレンマとは】ゲーム理論から考え方までわかりやすく解説

3章：ナッシュ均衡とパレート最適

最後に、ゲーム理論におけるパレート最適について確認してみましょう。

パレート最適（パレート効率的）とは、

とされています。（より詳しくは→【パレート最適とは】へ）

ゲーム理論においては誰かの犠牲がなければ、ほかの誰も利得を増やせない状態を指します。2章の囚人のジレンマの例を用いると、図４のように【2人とも否認する】がパレート最適となります。

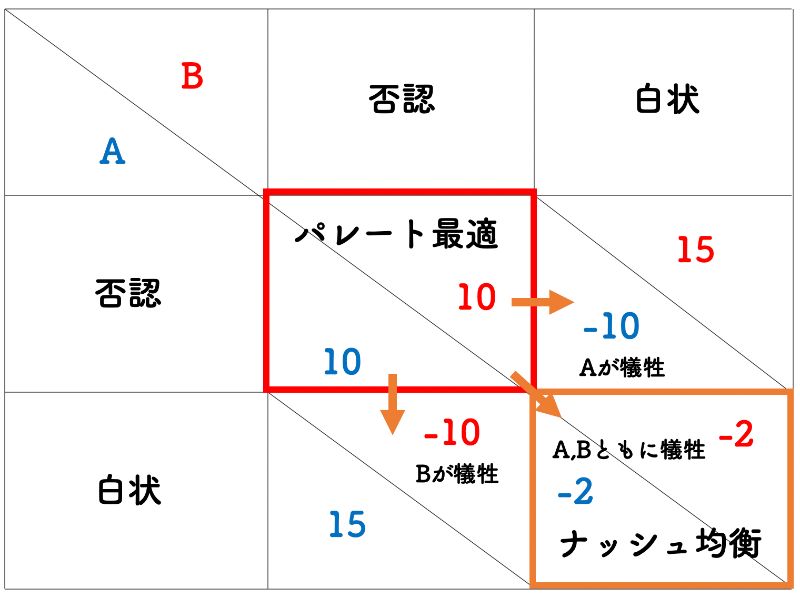（図４「ナッシュ均衡とパレート最適」出典: 筆者作成）

【2人とも否認する】という状況から他の３つの組み合わせに変化させようとすると、少なくても1人の利得が少なくなる、つまり誰かが犠牲になっていることがわかります。

パレート最適は、複数ある組み合わせのなかで全体の利得が最大となる組み合わせを導く方法であり、組み合わせの中でもっとも理想的な可能性であると言えます。

しかし、現実では1章や2章で説明したように、①互いにコミュニケーションが取れない、②相手の行動を思いめぐらせながら自分の行動を決める、という制約条件が存在するため、必ずしもパレート最適が選ばれるわけではありません。

どちらもさまざまな経済活動の分析に用いられる代表的な手法ですが、それぞれの手法の特徴を理解し、環境に合わせた適切な分析がおこなわれることが求められます。

^{Sponsored Link}

4章：ナッシュ均衡に関するおすすめ本

ナッシュ均衡を理解することはできましたか？

紹介した内容はあくまでも一部ですので、以下の書物を参考にさらに学びを深めていってください。

まとめ

最後にこの記事の内容をまとめます。