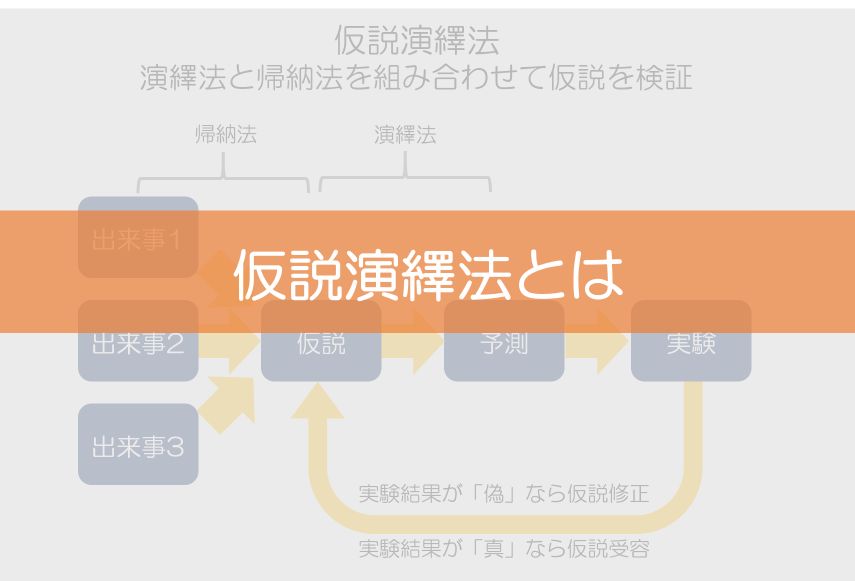
仮説演繹法(hypothetico deductive method)とは、帰納法によって仮説を提示し、仮説から実験可能な命題(予測)を演繹し、その予測が正しいかどうかを実験によって確かめる方法のことです。
仮説演繹法は、演繹法と帰納法の長所を組み合わせた推論の方法です。
ただし、仮説演繹法には問題点もあるため実際に方法論として使う場合は注意が必要です。
そこでこの記事では、
- 仮説演繹法の解説
- 仮説演繹法の例を使った解説
- 仮説演繹法とアブダクションの違い
など、実際に使えるように詳しく解説します。
関心のあるところから読んでみてください。
このサイトは人文社会科学系学問をより多くの人が学び、楽しみ、支えるようになることを目指して運営している学術メディアです。
ぜひブックマーク&フォローしてこれからもご覧ください。→Twitterのフォローはこちら
1章:仮説演繹法とは
もう一度整理しましょう。仮説演繹法とは、
- 経験的な事実から「仮説」を導き出す(帰納法)
- 仮説から実験可能な「予測」を導き出す(演繹法)
- 実験によって「予測」を確かめ、仮説の確かさを検証・反証する
という方法のことです。
これだけでは抽象的で分かりにくいと思いますので、まずは演繹法、帰納法の意味から説明し、それから仮説演繹法の具体的な流れを説明します。
このサイトでは複数の文献を参照して、記事を執筆しています。参照・引用箇所は注1ここに参照情報を入れますを入れていますので、クリックして参考にしてください。
1-1:演繹法と帰納法の問題点
そもそも演繹法(deduction-method)とは、「普遍的命題」から「個別的命題」を論理的に導き出すことです。また、帰納法(inductive method)とは、個々の経験的な事実から得られた「個別的命題」から「普遍的命題」を導き出すことです。
これらの推論の方法は古来から形成されてきたもので、形成される中でその特徴や問題点が浮き彫りになりました。
ここで重要なのは、演繹法にも帰納法にもそれぞれ問題点があるという点です。
詳しくは以下の記事で解説していますが、ここでは要点を整理します。
1-1-1:演繹法が抱える問題点
演繹法について簡単に言うと、すでに知られている前提や普遍的な法則から、結論や個別具体的な法則を導き出すことです。
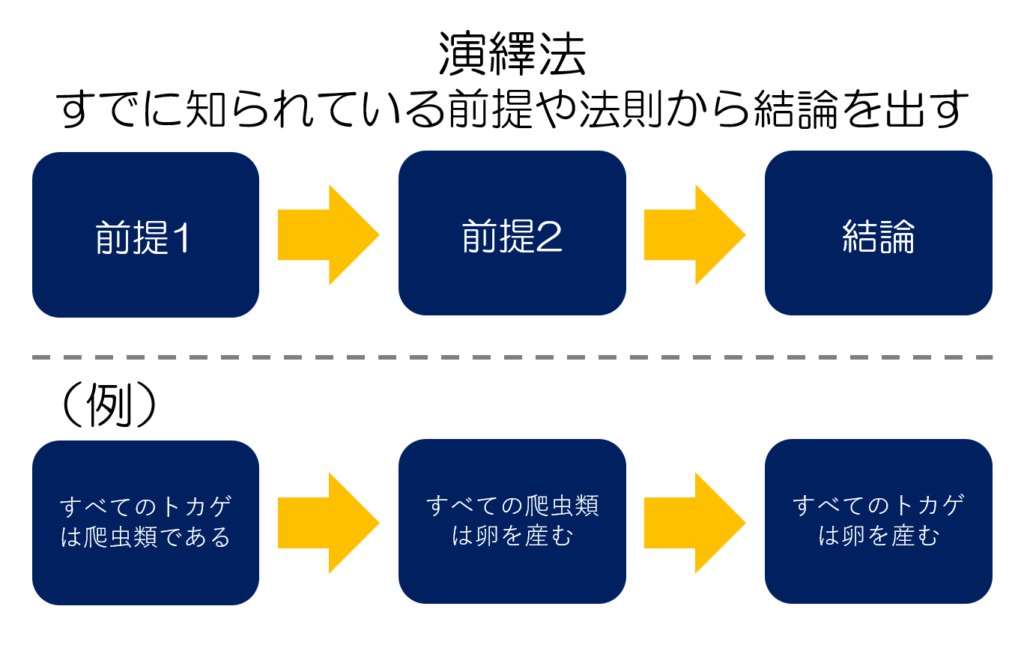
演繹法の特徴は、前提が正しければ必ず結論も正しい(真理保存性)ということです。しかし一方で、前提に結論となるものが含まれているということでもあるため、「新たな知識が得られない」という問題点もあります。
たとえば、上記の例にように「すべてのトカゲは爬虫類」「すべての爬虫類は卵を産む」ことが知られている世界で、すべてのトカゲが卵を産むことを主張しても、何も新しくありません。
1-1-2:帰納法が抱える問題点
帰納法について簡単に言うと、経験的に得られた事実や事例から、結論や普遍的な法則を導き出すということです。
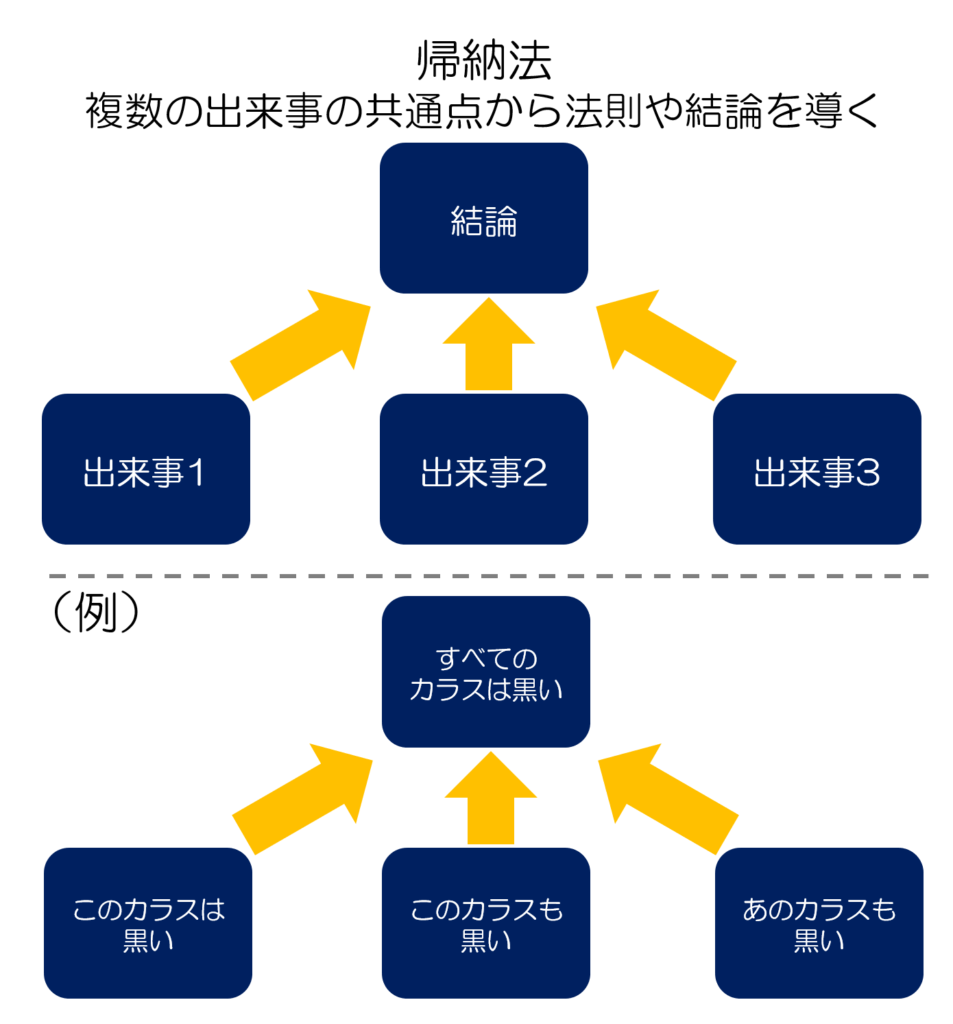
帰納法の特徴は、個別的な事例や出来事から結論を導き出すため、結論が論理的に必ず正しいとは言えないことです。
例えば、上記の例の場合、世界中のカラスを1匹残らず観察することはできないため、「すべてのカラスは黒い」という結論は必ず正しいとは言えません。「ある程度正しいだろう」という程度にしかなりません。
一方、帰納法は個別的な事例や事実から新しい法則や命題を導き出すことができるため、新しいことを明らかにできるメリットがあります。
これは演繹法にない強みです。
このように、演繹法と帰納法は一長一短なのです。学問の研究では、「正しい」ことと「新しい」ことがともに求められるため、演繹法と帰納法はともに活用することが求められます。
そこで考え出されたのが、仮説演繹法なのです。
1-2:仮説演繹法の実践方法
仮説演繹法はジョージ・ハーシェルが『自然哲学研究に関する予備的考察』(1930)で定式化し、その後18世紀~19世紀の科学者ウィリアム・ヒューエルや、19世紀の経済学者ウィリアム・ジェヴォンズらによって発展させられました2野家啓一『科学哲学への招待』ちくま学芸文庫119-125頁。
そして、整理された仮説演繹法の流れは以下の通りです。
- 観察による問題の発見
- 問題に対する仮説を作る(帰納)
- 仮説から実験可能な命題である「予測」を「演繹」する
- 「予測」を実験によって検証もしくは反証する
- 実験結果に基づいて仮説を受け入れるか、修正する
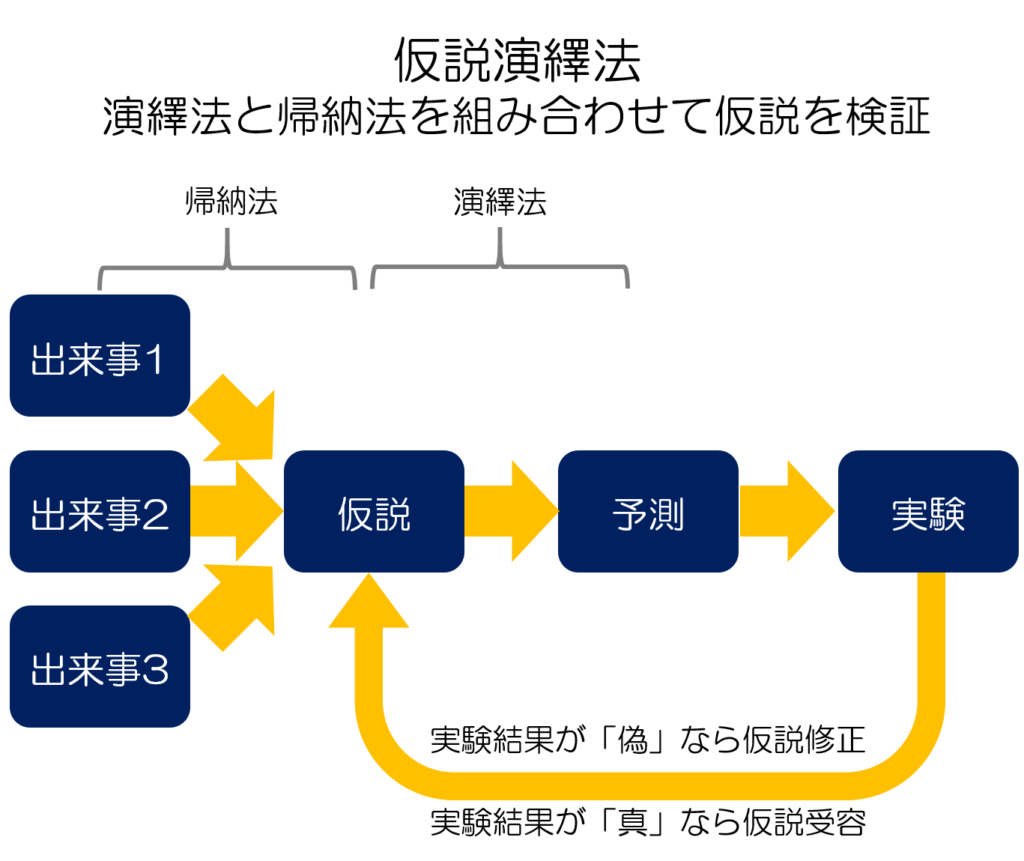
上記のように、問題を発見したらそれに対する仮説を帰納法によって導きだし、そこからさらに実験可能な「予測」を演繹法で導き出すのが仮説演繹法です。つまり、演繹法と帰納法を組み合わせることで、「正しさ」と「新しさ」を両立できるように考えられているのです。
ただし、仮説演繹法にも問題がないわけではありません
仮説演繹法も実験によって確かさを確認するのですから、実験による検証は帰納的です。そのため、実験結果が「予測が正しい」という結果でも、論理的に100%正しいとは言えず、一定の範囲で「確からしい」としか言えないのです。
とはいえ、演繹法や帰納法を単独で利用するよりも、新しい知識が得られてかつ確からしさを高められる点で、やはり仮説演繹法には意義があるのです。
まだ抽象的で分かりにくいかもしれませんので、2章では具体例を用いて説明します。
- 演繹法には「新しい知識が獲得できない」という問題点があり、帰納法には、結果が必ずしも論理的に正しいとは言えないという問題点がある
- 仮説演繹法は、帰納法によって仮説を作り、それを演繹法によって実験可能な予測にし、実験によって仮説を検証する手法
2章:仮説演繹法の例
さて、ここから仮説演繹法について具体例を用いて解説します。
戸田山和久の『科学哲学の冒険』という本では、仮説演繹法の代表例として「産褥熱(さんじょくねつ)」を用いて説明されています。とてもわかりやすいので、まずはこの例を元に解説します。
(2024/07/26 09:57:13時点 Amazon調べ-詳細)
「産褥熱」とは、イグナッツ・フィリップ・ゼンメルワイス(Ignaz Philipp Semmelweis)という医師によって「手を洗うことで感染症が防げる」ということが明らかにされた例です。
この例を先ほど紹介した、下記の仮説演繹法の流れから整理してみましょう。
- 観察による問題の発見
- 問題に対する仮説を作る(帰納)
- 仮説から実験可能な命題である「予測」を「演繹」する
- 「予測」を実験によって検証もしくは反証する
- 実験結果に基づいて仮説を受け入れるか、修正する
■仮説演繹法の例:産褥熱
医師のゼンメルワイスは、自分の病院で以下の事実を経験的に得ました。
- 多くのお産した女性が産褥熱で死亡していた
- しかも、産婆より医師が立ち会った場合の方が、女性が死亡することが多かった
- 医師は、解剖などで死体を触ることが多かった
まず、これが「①観察による問題の発見」です。
この事実から帰納法によって、死体に含まれる物質が体内に入っており、それが産褥熱の原因になると考えました。これが「②問題に対する仮説を作る(帰納)」です。
次に、「お産の前に手を洗うことで発生率が防げるかもしれない」という仮説を立てました。これは実験によって確かめることができるため「③仮説から実験可能な命題である予測を演繹する」です。
これは予測であるため、実験して確かめる必要があります。そこで、実際に手洗いを行って発生率を検証したところ、産褥熱の発生を抑えることができました。
これが「④予測を実験によって検証もしくは反証する」です。
こうして、手洗いという実験によって「予測」の確かさが分かったため、「仮説」が正しかったことが分かります。もし実験によって「予測」が間違っていることが分かれば、それは「仮説」が間違っていたことになります。
こうした手続きを経て問題の解決を図る推論の方法が、仮説演繹法です3※参考:戸田山和久の『科学哲学の冒険』(NHKブックス)。
このように、医師ゼンメルワイスは仮説演繹法を用いて、「手を洗うことで感染症を予防できる」ことを発見したのです。
先ほども説明したように、100回手を洗って予防できても101回目には予防できない可能性が論理的に残ってしまうという、帰納法の問題点は残されています。しかし、新しい予防法という知識を見つけ出すことができた点で、仮説演繹法という手法には大きな意義があるのです。
3章:仮説演繹法とアブダクション
仮説演繹法についてここまで説明してきましたが、仮説演繹法にも問題点があります。それは、仮説演繹法は「仮説を発見する方法」については教えてくれないということです。
そこで、仮説演繹法と似た方法として「アブダクション(abduction)」という方法が、哲学者のC・S・パース(Charles Sanders Peirce/1839-1914)によって提唱されました4野家、前掲書121頁。
3-1:アブダクションとは
アブダクション(abduction)とは、仮説を導き出すための推論の方法です。
パースはアブダクションの具体的な方法を整理していなかったのですが、後に哲学者N・R・ハンソンが『科学的発見のパターン』という書籍でアブダクションの方法を整理して提示しました。
ハンソンが提示したアブダクションの方法は以下のものです。
- ある変則的な現象が観測される
- とある仮説を「正しいもの(真)」とすると、①の変則的な現象を説明できる
- それゆえ、②の仮説を「正しいもの(真)」と考える理由がある
論理学について理解している方は、アブダクションの推論には問題があることが分かると思います。
整理すると、「現象Aが起こった。仮説Bがあれば『BならばA』として説明できる。ゆえに、Bは正しい」というのがアブダクションの推論ですが、これは仮説を前提として結論を導き出しているため、推論としては間違った結論になる可能性があるものです。
■アブダクションの例
A君は今年はじめて学校を欠席した。A君の欠席は、「A君がUFOにさらわれた」という仮説を立てると説明できる。ゆえに、「A君がUFOにさらわれた」という仮説には正しいと考えるべき理由がある。
この例を見れば分かる通り、アブダクションは推論としては論理的に間違う可能性が高いです。
しかし、ハンソンらアブダクションの支持者は、アブダクションに「正しい結果を導き出す」ことを期待したわけではありません。アブダクションは、仮説の発見法として有用性があると考えたのです。
もちろん、作った仮説は研究を進めるうちに間違っていることが分かることもあるのですが、その場合は再びアブダクションによって別の仮説を作れば良いのです。
このことから、アブダクションを社会科学の研究方法の一つとして重視する研究者もいます(3-2で紹介します)。
3-2:アブダクションと仮説演繹法の違い
ここまで読んで、「アブダクションと仮説演繹法って同じものでは?」と思われたかもしれません。しかし、繰り返しになりますがこの2つは異なる手法です。
アブダクションを社会科学の研究手法に活用することを提唱している、政治学者の保城広至は、アブダクションと仮説演繹法の違いを以下のように整理しています。
| 仮説演繹法 | アブダクション | |
| 推論の目的 | 仮説の検証 | 仮説の発見 |
| 方向づけ | (独立)変数から | 事例から |
| 事例の数 | 多数 | 少数 |
| 解明すべき条件 | 十分条件 | 必要条件 |
※保城広至『歴史から理論を創造する方法』p.90 をもとに作成
最大の違いは、仮説演繹法は仮説を実験によって「検証」することが目的であるのに対し、アブダクションは仮説を「発見」するために利用される手法である、という点です。
論理的に正しい推論の方法だけでは、仮説のアイディアが導き出せない場合に、非常に有用だと言えるのです。
- アブダクションとは、とある仮説を作ると起こった現象が説明できるという場合、その仮説を正しいものとして研究する意義がある、と考える方法
- 仮説演繹法が仮説の正しさを検証するものであるのに対して、アブダクションは仮説を「作り出す」手法
4章:仮説演繹法が学べる本
仮説演繹法は、さまざまな研究で取り入られています。
この記事で説明したのは、一般的な原則にすぎません。より詳しくはこれから紹介する書籍から学んでください。
戸田山和久『科学哲学の冒険ーサイエンスの目的と方法をさぐるー』(NHKBOOKS)
この本では、演繹法、帰納法、仮説演繹法、アブダクションを含むさまざまな推論の方法が、科学哲学の分野からとても分かりやすく説明されています。初心者でも読みやすい内容ですので、ぜひ読んでみてください。
(2024/07/26 09:57:13時点 Amazon調べ-詳細)
保城広至『歴史から理論を創造する方法ー社会科学と歴史学を統合するー』(勁草書房)
この本は、社会科学の「恣意的に事例をピックアップして理論化しがち」という問題と、歴史学の「記述重視で理論化を軽視しがち」という問題をクリアする、「中範囲の理論」という方法を提唱している本です。アブダクションが取り入れられており、アブダクションや仮説演繹法の手法について理解するのにも向いています。とてもいい本です。
(2024/07/25 18:47:40時点 Amazon調べ-詳細)
一部の書籍は「耳で読む」こともできます。通勤・通学中の時間も勉強に使えるようになるため、おすすめです。
最初の1冊は無料でもらえますので、まずは1度試してみてください。
また、書籍を電子版で読むこともオススメします。
Amazonプライムは、1ヶ月無料で利用することができますので非常に有益です。学生なら6ヶ月無料です。
数百冊の書物に加えて、
- 「映画見放題」
- 「お急ぎ便の送料無料」
- 「書籍のポイント還元最大10%(学生の場合)」
などの特典もあります。学術的感性は読書や映画鑑賞などの幅広い経験から鍛えられますので、ぜひお試しください。
まとめ
最後にこの記事の内容をまとめます。
- 仮説演繹法とは、帰納法によって事例から仮説を導き出し、その仮説から演繹法によって実験可能な予測を導き出し、実験によって仮説の正しさを検証する方法
- 仮説演繹法は、演繹法と帰納法のそれぞれの問題点をカバーできるが、実験によって確かめる点に、100%論理的に正しいとは言えない問題点もある
このサイトは人文社会科学系学問をより多くの人が学び、楽しみ、支えるようになることを目指して運営している学術メディアです。
ぜひブックマーク&フォローしてこれからもご覧ください。→Twitterのフォローはこちら