ベイズ統計学(Bayesian statistics)とは、18世紀の牧師トーマス・ベイズが発見したベイズの定理を用いることで、自分の直感を確率分布に反映させることができる統計学のことです。
ベイズ統計学は、近年はビッグデータの活用や機械学習のアルゴリズムに活用される場面が増えており、これから学ぶメリットは非常に大きいです。
ベイズ統計学は難解に見えますが、実はベイズの定理から順番に理解すれば、その基礎的な部分が理解できるようになっています。
そこでこの記事では、
- ベイズ統計学の基礎的な考え方
- ベイズ統計学と記述統計学、推計統計の違い
- ベイズの定理の導出やベイズ統計学の応用
- ベイズ統計学の問題点
について詳しく解説します。
読みたいところから読んでみてください。
このサイトは人文社会科学系学問をより多くの人が学び、楽しみ、支えるようになることを目指して運営している学術メディアです。
ぜひブックマーク&フォローしてこれからもご覧ください。→Twitterのフォローはこちら
1章:ベイズ統計学とは
「ベイズ統計学」という言葉、統計学を学んでいれば、誰しも一度は聞いたことがあると思います。とても難しそうに聞こえますよね。
また、高校数学で確率を勉強したことがある方は、
「「ベイズの定理」と何が違うんだ!?」
「もっと難しい概念が登場するのか!?」
と尚更身構えてしまうかもしれません。でも安心してください。ベイズ統計学で使う公式はただ一つ、
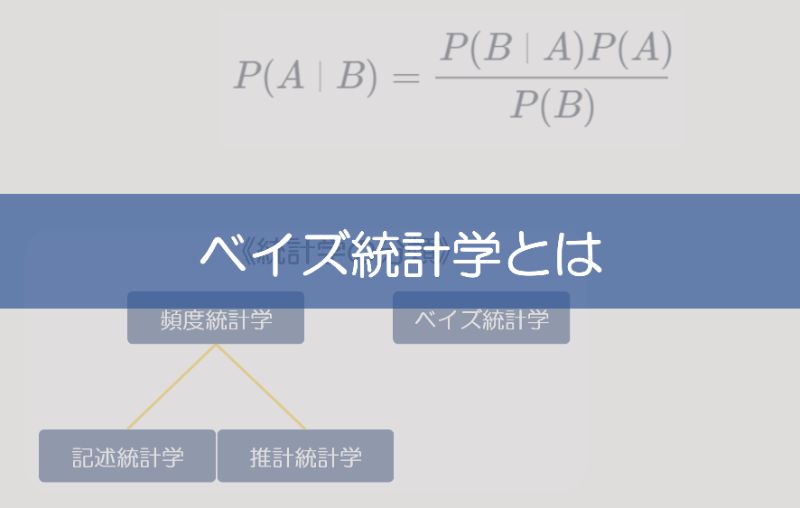
$$P(A│B)=\frac{P(B│A)P(A)}{P(B)} (1)$$
たったのこれだけ、高校数学で学習したベイズの定理そのものです。この公式にベイズ統計学のエッセンスが詰まっています。
1章では、ベイズ統計学の歴史や従来の頻度主義統計学との相違点、ベイズ統計学が活用されている分野について概観していきましょう。
1-1:ベイズ統計学の歴史
さて、まずは統計学の歴史を振り返ってみましょう。
初めて統計が行われたのはなんと紀元前3000年のピラミッド建設のための人口調査といわれています。ピラミッド建設に統計が使われていたなんて驚きですよね。このように統計学が学問として認知されるまで統計は国家のために人口や働き手を調べるための手段として使用されていました。
統計が学問として認知され始めたのは17世紀頃です。統計学の父と呼ばれるウィリアム・ペティの「政治算術」が発表され、以降統計学の研究が加速していきます。
その後も研究は進められ19世紀後半にフィッシャー・ネイマンらが頻度主義統計学(頻度主義統計学は次節で説明するので用語がわからなくても大丈夫です。)を大成させました。頻度主義統計学は徹底的に手続き化された為、統計学者ではないデータ分析家(自然科学者、人文科学者、社会学者など)に広く受け入れられ急速に広がり統計学の覇権を握りました。
では、そろそろ本題のベイズ統計学の歴史を見ていきましょう。
ベイズの定理の原型は1740年代頃にトーマス・ベイズという牧師が趣味の数学の研究をしている際に発見しました。しかし彼はそれを発表することなく亡くなってしまいます。
初めてベイズの定理が我々の知る(1)式の形で現れたのは19世紀初頭、ピエール・シモン・ラプラスによって発表された論文です。勘の良い方はお気づきだと思いますが実はベイズ統計学は頻度主義統計学より早く完成しているのです。
それにも関わらずベイズ統計は統計学の覇権を取ることが出来ませんでした。事前分布という確率分布のあいまいさが研究者の間で受け入れられず、また完璧に手続き化された頻度主義統計と比較してベイズ統計は複雑すぎて、データ分析者に拒絶されてしまったからです。
しかし近年、
- 従来のように複雑な計算をしなくともベイズの定理を使用できる方法の開発
- 計算機の速度向上
- メモリの大容量化
などからベイズ統計学が受け入れられ始め、今や頻度主義統計学と肩を並べています。
1-2:頻度主義統計学、ベイズ統計学の違い
では一体、頻度主義統計学とベイズ統計学はどう異なるのでしょうか。まずは以下の図をご覧ください。
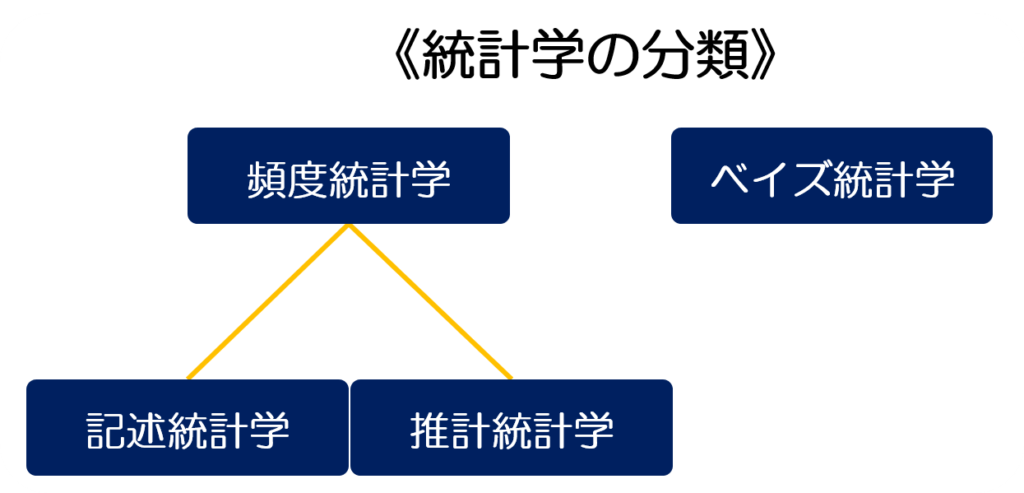
頻度主義統計学は記述統計と推計統計学に分かれておりベイズ統計学とは独立していますね。ではそれぞれの特徴を見ていきましょう。
1-2-1:記述統計学
記述統計学は最も古い統計学であり、大量の標本を用いてその集団の統計量を推測するものです。
例えば、
問題
自分の家族の平均身長はどのくらいですか?
という簡単な問題を記述統計学を用いて解いてみましょう。
これは簡単ですね。自分の家族全員の身長を測って平均すれば良いだけです。しかし、以下の問題はどうでしょうか?
問題
日本人の平均身長はどのくらいですか?
記述統計学を用いる場合この問題は解くのは(日本各地を旅して回り、全員の身長を測らない限り)不可能です。
このように記述統計ではすべての標本を集めるのが不可能な場合統計量を算出できないという欠点があります。
1-2-2:推計統計
推計統計は記述統計の欠点に対応するために発展した統計学です。具体的には母集団から標本を無作為に抽出して母集団の統計量を推計します。
では先ほどの問題、
問題
日本人の平均身長はどのくらいですか?
これを推計統計学を用いて解いてみましょう。
まず日本人を全国各地から無作為に抽出して(これが一番重要です。偏りが出ないように選ばなければなりません)、その人たちの身長を測って平均を取れば良いだけです。ちなみに今の問題では日本人全体が母集団、無作為に抽出した人たちが標本です。
このように推測統計学は母集団全てを集めることが不可能な場合でも標本を用いて母集団の統計量を推計することが出来ます。
しかし、推計統計学にも問題点があります。日本人の平均身長を推計した結果が以下のようになったとしましょう。
標本抽出した日本人の平均身長は190cmでした。
バスケットボール選手ばかり連れてきてしまったのでしょうか。これは直感的に高すぎますよね。しかし、推計統計学を使う以上、日本人の平均身長は190cmで決定!となってしまうのです。
このように推計統計学は推計しようとしているパラメータがある一つの真の値を持つと仮定しているため、偏りがある標本を抽出してしまうと誤った結論を出しやすいという欠点があります。
統計を勉強している学部生の方は、推計統計学にもパラメータの区間推定法があるから一つの真の値を仮定していないじゃないかと思われるかもしれません。
しかし区間推定法では「パラメータθが[α,β]にある確率が90%である」という表現は誤りで、正確には「データ解析を繰り返したとき、θが[α,β]にあるといえば90%くらいはあっているだろう」という表現になります。つまりθがある一つの真の値を持つと仮定しているのです。
Sponsored Link
1-2-3:ベイズ統計学
まず従来の頻度主義統計学とベイズ統計学で決定的に異なることは、下記の点です。
- 頻度統計学:パラメータはただ一点の真値を持つものとして捉え観測結果を得ることで、その一点を推定しようとする
- ベイズ統計学:パラメータがある確率分布に従うと捉え、観測結果を得ることでその確率分布を更新する
では先ほどの問題をベイズ統計学を利用して解いてみましょう。
ベイズ統計学ではまず、日本人の平均身長(ここではとおきます。)を確率分布として考えます。まず、我々が予想するの分布として
$$P(μ)$$
と予想します(これを事前に想定する分布という意味の事前分布と呼びます)。さて、ここで日本人全体から標本抽出して観測結果を得られたとしましょう。すると、その観測結果を踏まえた日本人の平均身長の確率分布として
$$P(μ│観測結果) (2)$$
という条件付確率として表現することが出来ます。この式どこかで見おぼえありますよね。そうです、ここでベイズの定理を使います。(2)式に対しベイズの定理を用いると、
$$P(μ│観測結果)=\frac{(P(観測結果|μ)P(μ))}{(P(観測結果))}∝P(観測結果|μ)P(μ) (3)$$
\(P(観測結果)\)は定数なのでこのように展開できます。\(P(μ│観測結果)\)を事後分布、\(P(観測結果|μ)\)を尤度と呼びます。観測結果を得ることで事前分布を事後分布に更新しているのです。
話は一旦戻りますが実は頻度主義統計学では尤度を最大にするパラメータを選ぶ最尤推定法という手法を用いて値を決定しています。つまり、先ほどの
標本抽出した日本人の平均身長は190cmでした。
という場合、頻度主義統計学では日本人の平均身長は190cmであると決定しますがこれは尤度が最大になるが190cmであるということなのです。
これに対し、ベイズ統計学ではパラメータの事後分布を考えることになりますので、例えば平均身長が190cmになる確率を知りたければ\(P(190cm│観測結果)\)の値を調べますし、160cmになる確率を知りたければ\(P(160cm│観測結果)\)の値を調べればよいのです
ベイズ統計学の立場ではバラメータを一点に決めるようなことはしないということです。
このように頻度主義統計学では結論は決定論的となりますが、ベイズ統計学では結論は確率的になります。
1-3:ベイズ統計学の現代における活用
2節でみたようにベイズ統計学は確率的な結論が可能になるので何かを判別する、分類するということに優れています。
例えば迷惑メール防止フィルタならば\(P(迷惑メールである│メール内の単語)\)、\(P(迷惑メールでない│メール内の単語)\)で迷惑メールであるか否かを判断します。
従来、事後確率は事前確率に共役事前分布と言う扱いやすい関数を用いなければ計算することは不可能でしたが、1節でも触れたように現代のコンピュータの処理速度向上により複雑な計算なしに事後分布を求めることが出来るようになっています(MCMC法)。
これは今日の主役であるビックデータと非常に相性がよく、大量のデータを用いて高精度の事後分布を再現することができ、マーケティングや心理学の分野でも応用されています。
また、機械学習法もベイズ統計学を用いて導出されているものが多いです。機械学習はそれで何冊も本が書けるほど難しく量も多いのでここでは割愛しますが、気になる方は是非『パターン認識と機械学習』上・下(丸善出版)を読んでみてください。機械学習アルゴリズムの多くがベイズ統計学を利用していることに驚くでしょう。
- ベイズ統計学の特徴は、パラメータがある確率分布に従うと捉え、観測結果を得ることでその確率分布を更新するという点
- ベイズ統計学は、ビッグデータや機械学習に活用されている
2章:ベイズ統計学の考え方
第一章ではいきなり事前分布や尤度が出てきて混乱してしまった方もいるかと思うのでこの章ではベイズ統計学の考え方について、ベイズの定理導入から説明していきます。
2-1:ベイズの定理導出
さて、いきなりですが今、あなたはサイコロを一つ中身の見えない箱の中で振ったとします。ここで奇数の目の出る確率を推測してみましょう。サイコロの奇数の目が出る事象をBとすると\(B= \{1,3,5\} \)となります。よって求める確率は
$$P(B)=\frac{3}{6}=\frac{1}{2}$$
となりますね。
次にあなたの友達が見えない箱の中身を見て2ではないと教えてくれたとしましょう。2出ないという事象は\(A=\{1,3,4,5,6\}\)となりますので、この場合の奇数の目が出る確率は\(\frac{3}{5}\)となります。この確率を条件付き確率と言い
$$P(B|A)=\frac{3}{5}$$
と表現します。ここで\(P(A)=\frac{5}{6}\)、\(P(A∩B)=\frac{3}{6}\)(奇数かつ2でない確率)であることを考えると\(P(B|A)\)は\(P(A∩B)\)を\(P(A)\)で割って求めていることが分かります。このように、条件付確率は一般的に以下のようにして求めることができます。
$$P(B|A)=\frac{P(A∩B)}{P(A)} (4)$$
(4)式を変形してみましょう。右辺の分母を両辺にかけると
$$P(B|A)P(A)=P(A∩B) (5)$$
となります。これが乗法定理です。
ここまで来ればベイズの定理の導出はできたも同然です。条件付確率の公式より
となります。第3式は乗法定理を利用しました。これがベイズの定理となります。
第一章でも説明しましたが、\(P(A│B)\)が事後分布、\(P(A)\)が事前分布、\(P(B|A)\)が尤度となります。Bを観測することによってAの確率分布を更新するイメージを持つと良いと思います。
2-2:ベイズ統計学応用①
それでは実際にベイズの定理を使ってみましょう。まずは第一章で用いた日本人の平均身長問題を考えます。なお、確率分布の概念に詳しくない方は無理に理解しようとせず第三節にお進み頂いて大丈夫です。ここでは
を再び使用します。この式を見てもわかる通り観測結果を得ることによりの確率分布を更新しています。
まずはの事前分布\(P(μ)\)を以下のように仮定します。
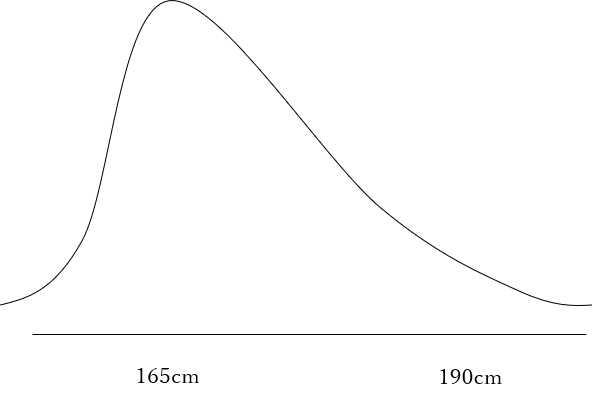
165cmにピークを持つ分布を想定しました。事前分布はこのように自分の直感で決定しても良いですし、何かの調査によって決定しても良いです。もちろん後者の方が信頼性は高くなります。
尤度は一般的に何かしらの確率分布を想定します。今回は\(P(観測結果|μ)\)は平均\(μ\)(厳密に計算するわけではないので分散は特に考えません)の正規分布に従うとしましょう。では実際に分布がどのように変化するのか見ていきます。
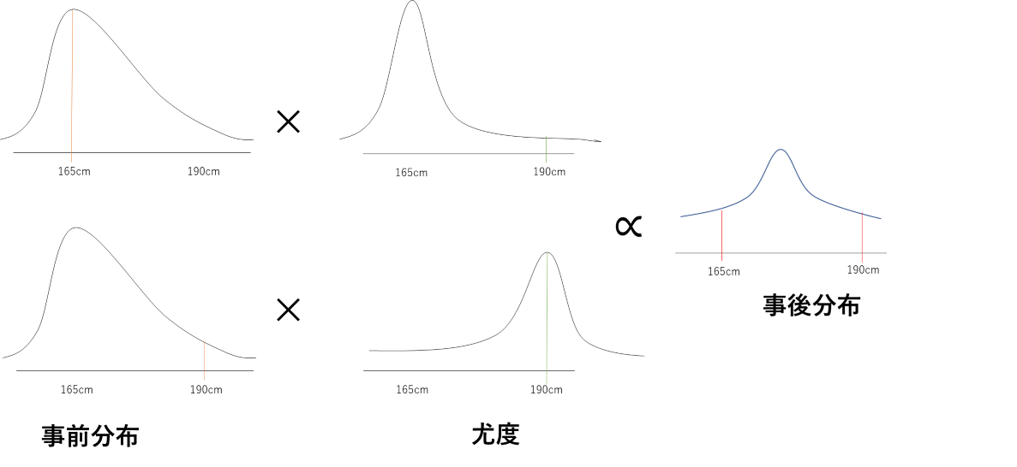
\(μ=165cm\)の事後確率は尤度が小さいため事前確率より小さくなり、\(μ=165cm\)の事後確率は尤度が大きいため事前確率より大きくなっています。結果として事後分布は事前分布の山(ピーク部分)が右に移動したような形になっています(事前分布では平均身長が165cm付近になると考えていましたが観測結果を受けて、事前分布が更新された結果、分布の山が190cm寄りに移動したと考えると良いでしょう。)。
頻度主義統計学では尤度が一番大きくなる190cmを日本人の平均身長だと決定してしまいますがベイズ統計学の立場に立って事後分布をみると少なくとも190cmと決定するのはおかしいぞと言えそうですね。
Sponsored Link
2-3:ベイズ統計学応用②
もっとわかりやすくベイズの定理を利用してみましょう。早速ですが問題です。
問題
総務省によると全受信メールに対する迷惑メールの割合は約40%だそうです。そこである研究者が「必ず当たります」というキーワードで迷惑メールを振り分けられないか調べたところ以下のようなことが分かりました。
各メールに「必ず当たります」が含まれている確率
| 迷惑メール | 非迷惑メール | |
| 必ず当たります | 0.2 | 0.05 |
さて、「必ず当たります」が入っていて迷惑メールである確率はどのくらいでしょう
一見簡単そうでよく考えてみると難しい問題なのですが実はベイズの定理を用いるとあっという間に解くことが出来ます。事前分布として総務省が調べた値を利用するとベイズの定理より、
となります。
キーワードについて調べる前、迷惑メールは(ランダムに選んで)40%でしか検出することはできませんでしたが「必ず当たります」というキーワードがあるか調べることで迷惑メールを72%で検出することが出来るようになりました。
このようにベイズの定理を用いることで得られた情報を基に事前分布を更新できることが分かります。
2-4:ベイズ統計学の問題点とその解決法
ベイズ統計学の問題点は何と言っても事前分布のあいまいさでしょう。
第二節で見た通り、ベイズの定理を用いることで自分の直感を確率分布に反映させることが出来ますが裏を返せば適当に事前分布を選んでしまうこともできるわけです。これでは厳密性を重んじる学者達に受け入れられてこなかったのも納得できます。
この問題はベイズ更新という手法を用いることで可決できます。ベイズ更新とは情報が加わるたびに確率分布を以下のように更新していくことです。ただし、情報はB,C,Dの順で与えられるものとします。
$$P(A│B)=\frac{P(B│A)P(A)}{P(B)}=P(F_1)$$
$$P(A│B,C)=\frac{P(A│C)P(F_1)}{P(C)}=P(F_2)$$
$$P(A│B,C,D)=\frac{P(A│D)P(F_2 )}{P(D)}$$
このように事後分布として算出された分布を次の時点の事前分布として用いることで情報の逐次更新が可能になります。
我々の主観で決定することのできる分布は\(P(A)\)ですが情報が与えられるにつれて影響が小さくなっていくことが分かります。現在はビックデータを高速に扱うことのできるためベイズ更新を繰り返せば事前確率の影響はほぼなくなり、様々な分野でベイズ統計学が使われるようになっています。
3章:ベイズ統計学が学べるおすすめ本
ベイズ統計学について理解することはできましたか?
ここで説明したのは、ベイズ統計学の基礎的なことに過ぎません。より詳しくは、以下の書籍から学びを深めてみてください。
オススメ度★★★小島寛之『完全独習 ベイズ統計学入門』(ダイヤモンド社)
この本はベイズ統計学について初心者向けにとてもわかりやすく書かれた入門書です。統計学の基礎から知りたい場合は、同シリーズの『完全独習統計学』から読み、こちらの本に進むことをおすすめします。
オススメ度★★豊田秀樹『基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門』(朝倉書店)
これもベイズ統計学の本格的な入門書として非常に優れています。ベイズ統計学を学ぶなら必読書です。ただし、ある程度の統計学の基礎知識を前提としていますので、前述の2冊の内容は頭に入れた上で読むことをおすすめします。
(2021/09/30 00:08:08時点 Amazon調べ-詳細)
一部の書籍は「耳で読む」こともできます。通勤・通学中の時間も勉強に使えるようになるため、おすすめです。
最初の1冊は無料でもらえますので、まずは1度試してみてください。
また、書籍を電子版で読むこともオススメします。
Amazonプライムは、1ヶ月無料で利用することができますので非常に有益です。学生なら6ヶ月無料です。
数百冊の書物に加えて、
- 「映画見放題」
- 「お急ぎ便の送料無料」
- 「書籍のポイント還元最大10%(学生の場合)」
などの特典もあります。学術的感性は読書や映画鑑賞などの幅広い経験から鍛えられますので、ぜひお試しください。
まとめ
最後にこの記事の内容をまとめます。
- ベイズ統計学は頻度統計学(記述合計額、推計統計学)と違い、パラメータがある確率分布に従うと捉え観測結果を得ることでその確率分布を更新すること
- ベイズ統計学には、事前分布があいまいであるという問題点があるものの、「ベイズ更新」という手続きで解決されている
このサイトでは、他にも統計学のテーマについて解説していきますので、ぜひブックマークしてください。