【フレーミング効果とは】プロスペクト理論との関係からわかりやすく解説

フレーミング効果は私たちの意思決定を理解する上で重要な理論の一つです。

この記事では、

• フレーミング効果の意味・例
• フレーミング効果の学術的な議論

をそれぞれ解説していきます。

好きな箇所から読み進めてください。

１章：フレーミング効果とは

１章では、フレーミング効果を概説します。フレーミング効果とプロスペクト理論の関係に関心のある方は、２章から読んでみてください。

1-1：フレーミング効果の意味

冒頭の確認となりますが、フレーミング効果とは、

です。

このフレーミング効果について理解するためには、「心理学における規範的な意思決定」と「フレーミング効果が生じる場面」を理解する必要があります。

1-1-1：心理学における規範的な意思決定

１点目は、規範的な意思決定というものが心理学ではどのように考えられているかという点です。意思決定の研究における規範的な意思決定の理論として期待効用理論があります。

期待効用理論とは、

です。

この理論では、私たちはある不確実性の伴う状況下である意思決定を行う際に、効用の期待値の大きい選択をすると仮定されます。

効用の期待値について詳しく説明したいと思います。

しかし、意思決定の場面というのはこのような確実な選択ばかりではありません。25％の確率で100万円を受け取れるくじを引くか、90％の確率で50万円をうけとれるくじを引くかどちらにするかといったような不確実性の介在する場面も存在します。

このような場面で役に立つのが、期待値という考え方です。

つまり、後者のほうが期待値が高いので後者を私たちが選択するだろうということをこの期待効用理論では説明してくれているわけです。

1-1-2：フレーミング効果が生じる場面

2点目は、フレーミング効果がどのような場面で生じるかという点です。期待効用理論に基づけば、期待値が同じであればどのような文脈でも同じ判断をするはずです。

しかし、意思決定の場面においては、得られる効用やその確率のほかにさまざまな文脈が提示されます。下記の問題を行ってみてください。

それぞれのパターンで選択した対策を覚えておいてください。この問題は、トヴェルスキーとカーネマンという心理学者が行った実験に使用された問題の1つです。

この問題の特徴は、すべての対策がもたらす効用は同じに設定されているという点と、パターン１とパターン2はフレーミングを変えただけで同じ判断をさせているという点です。

まず、前者について考えてみましょう。わかりやすいようにすべての対策の利得と損失について分けて考えてみましょう。

まず、利得を求めます。利得とは助かる人数の期待値です。

次に損失を求めましょう。損失とは死んでしまう人数の期待値です。

このように整理すると、どの対策も得られる利得も損失も同じ値であり、期待効用理論に基づくと規範的には同じ値を持つ対策ということになります。

続いて、後者の特徴について考えてみましょう。先ほどの問題は、パターン1では利得に着目させるように、パターン2では損失に着目させるように文章が書かれていました。

つまり、パターン１は利得にフレーミングされた問題、パターン２は損失にフレーミングされた問題だったということです。先ほどの計算に対応させて考えてみると以下のようになります。

利得の計算

損失の計算

このように整理すると、対策Aと対策C、対策Bと対策Dがそれぞれ対応していることがわかります。

すべての対策の期待効用は同じですので、「対策Aと対策C」のような大きなリスクを取らない選択をするのか、「対策Bと対策D」のような大きなリスクをとる選択をするのかは個人の好みによって決定すると考えられます。

つまり、以下のことがいえます。

しかし、トヴェルスキーとカーネマンの実験では、パターン１では約70%程度の回答者が対策Aを選択し、パターン２では約80%程度の回答者が対策Dを選択しました。つまり、パターン1とパターン２で参加者の判断の選好が逆転したということです²Kahneman, D., & Tversky, A. (2013). Prospect theory: An analysis of decision under risk. In Handbook of the fundamentals of financial decision making: Part I (pp. 99-127)。

このことは、利得に着目させられるか損失に着目させられるかによって私たちの意思決定の傾向が異なるということを意味しています。

すなわち、規範的には同じ決定をしているような場面でも異なる文脈が与えられると異なる判断をしてしまうというフレーミング効果が見られたということです。

1-２：フレーミング効果の例

このようなフレーミング効果ですが、現実場面でもさまざまな状況でみられます。たとえば、売り出したい商品のチラシを作るような場合を考えてみましょう。

この情報を伝える方法には２つの言い方があります。「99％のウイルスを除菌できます」と「１％のウイルスが除菌できません」です。どちらも規範的には同じことを言っていますが、後者の販売文句はおそらく市場では見たことないでしょう。

このように、フレーミング効果は市場における広告などを考える際に非常に重要な概念の1つとして利用されています。

フレーミング効果は、心理学においては利得と損失フレーミングの違いが意思決定に与える効果のことを指します。

その意味で、「ものは言いよう」といったこととは少し異なるのですが、この効果はものの言い方ひとつで私たちの意思決定は大きく変わるということを意味しています。

2章：フレーミング効果の理論的説明としてのプロスペクト理論

では私たちはなぜ、フレーミング効果に見られたようなあべこべな判断を行ってしまうのでしょうか？そのことを説明したのがプロスペクト理論です。

2-1：価値関数と確率荷重関数

プロスペクト理論はこのような利得と損失に対する意思決定の違いを2つの観点から、説明してくれます。その1つが「価値関数」でもう1つが「確率荷重関数」と呼ばれるものです。

それぞれ「関数」というくらいなので、それぞれ数式として定義されているのですが、ここではその説明は省略します。プロスペクト理論ではこれら２つの関数に基づいて図1のような関係が示されています。

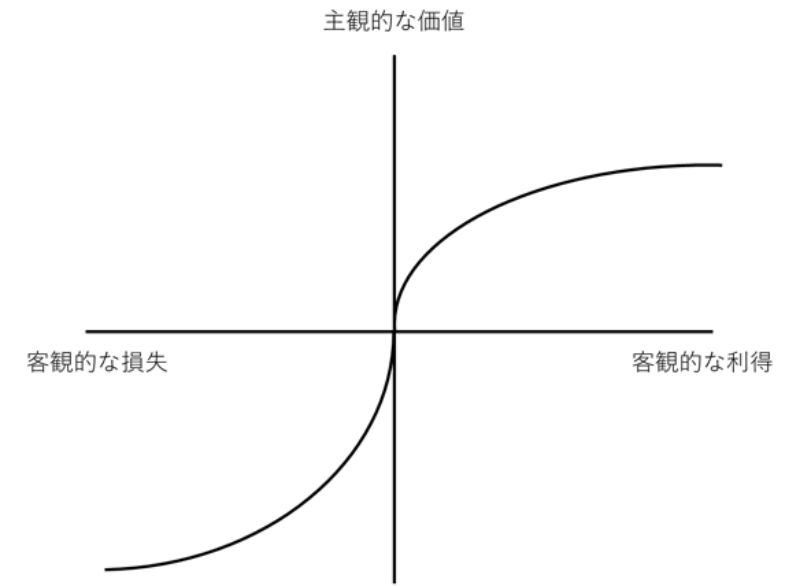図1　プロスペクト理論の価値関数のグラフ（注：手書きのため、正確なプロスペクト理論のグラフではありません。）

縦軸は主観的な価値の大きさを、横軸は客観的な利得や損失を表しています。このグラフの特徴は、利益が得られるときと、損失が生じるときとではその傾きが異なることです。図2をご覧ください。

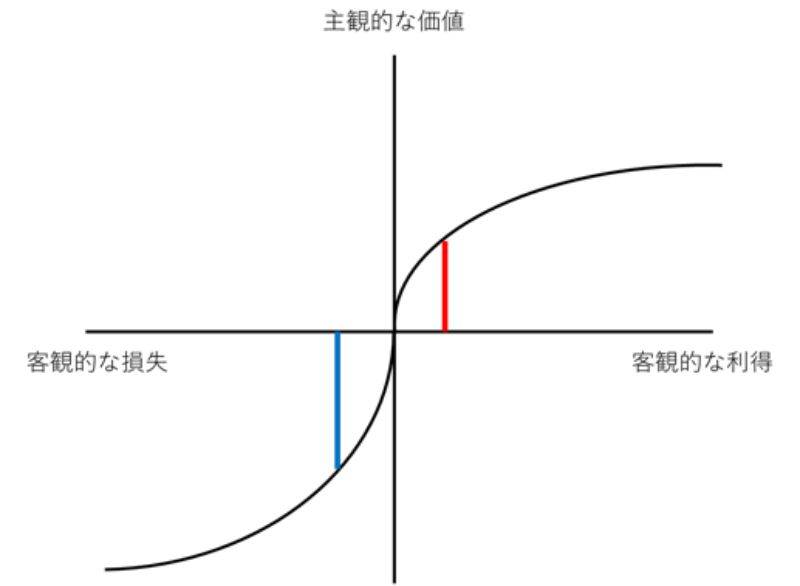図２ 利得と損失に対する主観的価値の違い（注：手書きのため、正確なプロスペクト理論のグラフではありません。）

図2における、赤と青の線はそれぞれｘ軸から同じ距離にあります。わかりやすく言えば、利得40万円が赤い線、損失40万円が青い線です。

主観的な価値が上に行くほど価値が高い、下に行くほど価値が低いので、このモデルでは利得と損失が客観的に同じであっても、損失のほうが大きく見積もられることがわかります。

このプロスペクト理論のグラフにおいて重要な特徴は、以下の２点です。

これにより、プロスペクト理論は期待効用だけでは説明が出来なかった、人間の不合理な意思決定を説明するものなのです。（→より詳しくはこちらの記事）

2-２：感応度逓減

プロスペクト理論によって説明される私たちの損失利得判断の性質として重要な要素がもう1つあります。それは、感応度逓減（diminishing sensitivity）です。

グラフを見るとわかりますが、利得も損失もその量が増えれば増えるほど傾きがなだらかになっているのがわかります。これは私たちが利得や損失が小さいときにはその差に敏感だが、大きくなるとその差に対する感度が鈍くなることを意味しています。

たとえば、次の２つの例を考えてみてください。

この場合、100万円のときほどがっかりしていないのではないでしょうか？これのもらえるの部分を罰金されるに言い換えても同じように感じると思います。

このように私たちは、利得や損失に対する感度が大きくなればなるほどその変化量に対する感度が低くなって（逓減して）いきます。この性質のことを感応度逓減といいます。

このプロスペクト理論に基づいてフレーミング効果について考えてみましょう。まずパターン1の問題では「確実に利得を得る対策Aか利得は大きいが損失を含む対策Bを選択する」という文脈における判断になります。

プロスペクト理論に基づくと、私たちは損失を回避する傾向にありますので、損失が一見ないように見える対策Aを選択すると考えられます。またパターン２「確実な損失のある対策Cと損失を回避できる可能性のある対策Dを比べる」という文脈における判断になります。

そのため、損失を回避できる可能性がある対策Dが選ばれると考えられます。このように、プロスペクト理論に基づくことで、フレーミング効果による非合理的な判断の一部を説明できるというわけです。

３章：フレーミング効果を学ぶ本・論文

フレーミング理論を理解することはできましたか？最後に、あなたの学びを深めるためのおすすめ書物を紹介します。

まとめ

最後にこの記事の内容をまとめます。